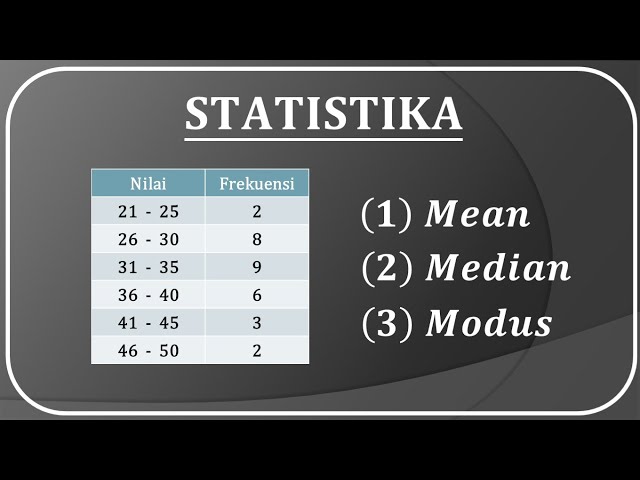
Cara menentukan mean adalah proses menemukan nilai rata-rata dari sekumpulan data. Mean juga dikenal sebagai rata-rata aritmatika atau rata-rata. Untuk menentukan mean, kita menjumlahkan semua nilai dalam kumpulan data dan kemudian membaginya dengan jumlah nilai tersebut. Misalnya, jika kita memiliki kumpulan data {1, 2, 3, 4, 5}, meannya adalah (1 + 2 + 3 + 4 + 5) / 5 = 3.
Mean adalah ukuran tendensi sentral yang penting. Hal ini dapat digunakan untuk membandingkan kumpulan data yang berbeda dan untuk mengidentifikasi tren dan pola. Mean juga digunakan dalam banyak aplikasi statistik, seperti analisis regresi dan pengujian hipotesis.
Artikel ini akan membahas berbagai metode untuk menentukan mean, termasuk metode manual dan metode menggunakan perangkat lunak statistik. Artikel ini juga akan membahas pentingnya mean dan penggunaannya dalam statistik.
Cara menentukan mean
Menentukan mean adalah proses penting dalam statistik yang melibatkan beberapa aspek penting, yaitu:
- Data: Kumpulan nilai yang akan dihitung meannya.
- Jumlah: Total nilai dalam kumpulan data.
- Pembagian: Proses membagi jumlah dengan jumlah nilai dalam kumpulan data.
- Rata-rata: Hasil pembagian, yang merupakan nilai mean.
- Tren: Mean dapat digunakan untuk mengidentifikasi tren dan pola dalam kumpulan data.
- Pengambilan keputusan: Mean dapat membantu dalam pengambilan keputusan berdasarkan data.
- Statistik inferensial: Mean adalah dasar dari banyak teknik statistik inferensial.
Dengan memahami aspek-aspek ini, kita dapat menentukan mean secara akurat dan menggunakannya secara efektif dalam analisis data. Misalnya, dalam kumpulan data nilai ujian, mean dapat membantu kita mengidentifikasi siswa dengan nilai rata-rata atau di atas rata-rata. Mean juga dapat digunakan untuk membandingkan kinerja siswa di kelas yang berbeda atau pada waktu yang berbeda.
Data
Data merupakan kumpulan nilai yang menjadi dasar untuk menghitung mean. Tanpa data, tidak mungkin menentukan mean. Data dapat berupa angka, pengukuran, atau nilai lainnya yang dapat dikuantifikasi. Misalnya, jika kita ingin menghitung mean nilai ujian siswa, kumpulan data kita adalah nilai ujian masing-masing siswa.
Kualitas data sangat penting untuk menentukan mean yang akurat. Data harus lengkap, akurat, dan relevan. Jika data tidak lengkap atau akurat, mean yang dihasilkan akan bias dan tidak dapat diandalkan. Misalnya, jika beberapa siswa tidak mengikuti ujian, mean nilai ujian akan lebih tinggi dari nilai sebenarnya karena hanya mencakup siswa yang mengikuti ujian.
Memahami hubungan antara data dan mean sangat penting untuk melakukan analisis data yang akurat dan bermakna. Ini memungkinkan kita untuk menafsirkan hasil dengan benar dan membuat keputusan berdasarkan data yang dapat diandalkan.
Jumlah
Dalam konteks “cara menentukan mean”, jumlah memainkan peran krusial karena merupakan dasar perhitungan mean. Jumlah diperoleh dengan menjumlahkan semua nilai dalam kumpulan data. Tanpa jumlah yang akurat, mean yang dihasilkan akan salah dan menyesatkan.
-
Menghitung Total Semua Nilai:
Langkah pertama dalam menghitung mean adalah menjumlahkan semua nilai dalam kumpulan data. Misalnya, jika kita memiliki kumpulan data {1, 2, 3, 4, 5}, jumlahnya adalah 1 + 2 + 3 + 4 + 5 = 15.
-
Jumlah dan Ukuran Kumpulan Data:
Jumlah dipengaruhi oleh ukuran kumpulan data. Semakin besar kumpulan data, semakin besar pula jumlahnya. Ini karena jumlah mencakup semua nilai dalam kumpulan data, terlepas dari jumlahnya.
-
Pengaruh Nilai Ekstrem:
Nilai ekstrem dalam kumpulan data dapat berdampak signifikan pada jumlah. Nilai ekstrem yang tinggi dapat meningkatkan jumlah, sedangkan nilai ekstrem yang rendah dapat menurunkannya. Oleh karena itu, penting untuk mempertimbangkan dampak nilai ekstrem saat menafsirkan jumlah.
-
Menghindari Kesalahan Perhitungan:
Kesalahan perhitungan saat menjumlahkan nilai dapat menyebabkan jumlah yang salah. Kesalahan ini dapat terjadi karena kesalahan manusia atau kesalahan perangkat lunak. Memeriksa ulang perhitungan sangat penting untuk memastikan jumlah yang akurat.
Memahami hubungan antara jumlah dan cara menentukan mean sangat penting untuk menghitung mean yang akurat dan andal. Jumlah memberikan dasar untuk perhitungan mean, dan mempertimbangkan faktor-faktor yang memengaruhi jumlah dapat membantu kita menafsirkan dan menggunakan mean dengan benar.
Pembagian
Pembagian merupakan langkah penting dalam menentukan mean karena memungkinkan kita memperoleh nilai rata-rata dari kumpulan data. Proses pembagian ini melibatkan pembagian jumlah, yang merupakan total semua nilai dalam kumpulan data, dengan jumlah nilai dalam kumpulan data tersebut.
Sebagai contoh, jika kita memiliki kumpulan data {1, 2, 3, 4, 5}, jumlahnya adalah 15 dan jumlah nilai adalah 5. Melalui pembagian, kita memperoleh mean 15 / 5 = 3. Nilai ini mewakili nilai rata-rata dari kumpulan data tersebut.
Memahami konsep pembagian dalam konteks menentukan mean sangat penting karena memberikan dasar untuk menghitung nilai rata-rata secara akurat. Proses pembagian ini memastikan bahwa setiap nilai dalam kumpulan data memiliki bobot yang sama dalam menentukan mean, sehingga menghasilkan representasi yang adil dan andal dari nilai rata-rata.
Rata-rata
Rata-rata merupakan hasil dari pembagian jumlah dengan banyaknya data, dan merupakan inti dari “cara menentukan mean”. Konsep rata-rata sangat penting dalam statistika, yang memberikan ukuran tendensi sentral dari suatu kumpulan data, serta gambaran yang jelas tentang nilai tipikal dalam kumpulan tersebut.
-
Nilai Representatif:
Rata-rata mewakili nilai yang paling sering muncul dalam suatu kumpulan data, menjadikannya ukuran yang dapat diandalkan untuk menggambarkan kecenderungan keseluruhan data. Sebagai contoh, jika kita memiliki kumpulan nilai ujian {70, 80, 90, 85, 88}, rata-ratanya adalah 82,6. Nilai ini menunjukkan bahwa sebagian besar siswa memperoleh nilai sekitar 82,6 pada ujian tersebut.
-
Pengambilan Keputusan:
Rata-rata dapat membantu dalam pengambilan keputusan dengan menyediakan dasar untuk perbandingan. Misalnya, jika kita membandingkan rata-rata nilai ujian dua kelas, kita dapat mengidentifikasi kelas dengan kinerja yang lebih baik secara keseluruhan. Informasi ini dapat digunakan untuk mengalokasikan sumber daya atau menerapkan strategi pengajaran yang lebih efektif.
-
Analisis Tren:
Rata-rata dapat digunakan untuk menganalisis tren dari waktu ke waktu. Dengan membandingkan rata-rata dari kumpulan data yang dikumpulkan pada waktu berbeda, kita dapat mengidentifikasi perubahan atau pola dalam data tersebut. Misalnya, dengan membandingkan rata-rata nilai ujian siswa dari tahun ke tahun, kita dapat memantau kemajuan atau penurunan kinerja siswa secara keseluruhan.
-
Dasar Statistika Inferensial:
Rata-rata merupakan dasar dari banyak teknik statistika inferensial, seperti pengujian hipotesis dan estimasi interval. Dengan menggunakan rata-rata, kita dapat membuat kesimpulan tentang populasi yang lebih besar berdasarkan sampel data yang lebih kecil.
Dengan memahami hubungan antara rata-rata dan “cara menentukan mean”, kita dapat memperoleh wawasan yang lebih baik tentang kumpulan data, membuat keputusan yang tepat, dan menerapkan teknik statistika inferensial dengan benar. Rata-rata merupakan ukuran yang sangat berharga dalam statistika, yang memungkinkan kita untuk meringkas dan menafsirkan data secara efektif.
Tren
Dalam konteks “cara menentukan mean”, hubungan antara tren dan mean sangat penting karena memungkinkan kita memperoleh wawasan yang lebih dalam dari kumpulan data. Mean dapat mengungkapkan perubahan atau pola dari waktu ke waktu, membantu kita mengidentifikasi tren yang mendasari dan membuat prediksi yang lebih baik.
-
Deteksi Perubahan:
Mean dapat digunakan untuk mendeteksi perubahan yang signifikan dalam suatu kumpulan data. Misalnya, dengan membandingkan mean nilai ujian siswa dari tahun ke tahun, kita dapat mengidentifikasi peningkatan atau penurunan kinerja siswa secara keseluruhan. Informasi ini dapat memicu penyelidikan lebih lanjut untuk menentukan penyebab perubahan dan mengambil tindakan yang sesuai.
-
Prediksi Tren:
Mean dapat digunakan untuk memprediksi tren di masa depan dengan mengidentifikasi pola dalam data historis. Misalnya, dengan menganalisis mean penjualan bulanan selama beberapa tahun, kita dapat memprediksi tren penjualan untuk bulan-bulan mendatang. Prediksi ini dapat membantu bisnis membuat keputusan yang tepat mengenai produksi, persediaan, dan strategi pemasaran.
-
Analisis Musiman:
Mean dapat digunakan untuk menganalisis pola musiman dalam kumpulan data. Misalnya, dengan menghitung mean suhu harian sepanjang tahun, kita dapat mengidentifikasi bulan-bulan terpanas dan terdingin. Informasi ini dapat berguna untuk perencanaan dan pengambilan keputusan di berbagai industri, seperti pariwisata dan pertanian.
-
Korelasi Tren:
Mean juga dapat digunakan untuk mengidentifikasi korelasi antara tren yang berbeda dalam kumpulan data. Misalnya, dengan membandingkan mean nilai ujian siswa dengan mean kehadiran mereka, kita dapat mengidentifikasi hubungan antara kehadiran dan kinerja akademik. Pemahaman tentang korelasi ini dapat membantu mengembangkan strategi untuk meningkatkan hasil siswa.
Dengan memahami hubungan antara tren dan “cara menentukan mean”, kita dapat memperoleh wawasan yang berharga dari kumpulan data, mengidentifikasi peluang, dan membuat keputusan yang lebih baik. Mean adalah alat yang ampuh untuk mengungkap tren dan pola, memungkinkan kita untuk memahami data secara lebih komprehensif dan membuat prediksi yang lebih akurat.
Pengambilan keputusan
Dalam konteks “cara menentukan mean”, hubungan antara pengambilan keputusan dan mean sangat penting karena memungkinkan kita untuk menggunakan data untuk menginformasikan keputusan dan membuat pilihan yang lebih baik.
Mean memberikan ukuran kuantitatif dari kumpulan data, yang dapat digunakan sebagai dasar perbandingan dan evaluasi. Misalnya, seorang manajer dapat menghitung mean kinerja penjualan timnya untuk mengidentifikasi individu atau tim dengan kinerja terbaik. Informasi ini dapat digunakan untuk mengambil keputusan mengenai alokasi sumber daya, penghargaan, atau pelatihan.
Selain itu, mean dapat digunakan untuk mengidentifikasi tren dan pola dalam data. Misalnya, sebuah perusahaan dapat menghitung mean penjualan bulanan selama beberapa tahun untuk mengidentifikasi bulan-bulan dengan penjualan tertinggi dan terendah. Informasi ini dapat membantu perusahaan membuat keputusan mengenai produksi, persediaan, dan strategi pemasaran.
Dengan memahami hubungan antara pengambilan keputusan dan “cara menentukan mean”, kita dapat memanfaatkan data untuk membuat keputusan yang lebih tepat dan efektif. Mean menyediakan dasar kuantitatif untuk perbandingan, evaluasi, dan identifikasi tren, sehingga memungkinkan kita untuk mengalokasikan sumber daya secara lebih efisien, mengoptimalkan strategi, dan pada akhirnya mencapai hasil yang lebih baik.
Statistik inferensial
Dalam konteks “cara menentukan mean”, hubungan antara statistik inferensial dan mean sangat penting karena memungkinkan kita untuk membuat kesimpulan tentang populasi yang lebih besar berdasarkan sampel data yang lebih kecil. Mean memberikan dasar untuk teknik statistik inferensial, seperti pengujian hipotesis dan estimasi interval.
-
Pengujian Hipotesis:
Pengujian hipotesis adalah teknik statistik yang digunakan untuk menentukan apakah terdapat perbedaan yang signifikan antara dua atau lebih kelompok. Mean digunakan untuk membandingkan kelompok-kelompok ini dan menentukan apakah perbedaan di antara mereka cukup besar untuk dianggap signifikan secara statistik atau hanya terjadi karena kebetulan.
-
Estimasi Interval:
Estimasi interval adalah teknik statistik yang digunakan untuk memperkirakan suatu parameter populasi, seperti mean, dengan tingkat kepercayaan tertentu. Mean digunakan sebagai titik tengah dari interval kepercayaan, yang memberikan kisaran nilai di mana parameter populasi diperkirakan berada.
Dengan memahami hubungan antara statistik inferensial dan “cara menentukan mean”, kita dapat menggunakan data sampel untuk membuat kesimpulan yang lebih luas dan andal tentang populasi yang lebih besar. Statistik inferensial memungkinkan kita untuk menguji hipotesis, memperkirakan parameter populasi, dan membuat prediksi dengan tingkat kepercayaan tertentu, sehingga membantu kita memperoleh wawasan yang lebih dalam dari data.
Tutorial Cara Menentukan Mean
Mean, atau rata-rata, merupakan ukuran tendensi sentral yang penting dalam statistika. Mean digunakan untuk meringkas kumpulan data dengan memberikan nilai tunggal yang mewakili nilai tipikal. Berikut adalah tutorial langkah demi langkah tentang cara menentukan mean:
-
Langkah 1: Kumpulkan Data
Kumpulkan semua data yang relevan dengan masalah yang sedang Anda analisis. Pastikan datanya lengkap dan akurat.
-
Langkah 2: Jumlahkan Semua Nilai
Jumlahkan semua nilai dalam kumpulan data. Pastikan untuk menjumlahkan semua nilai, termasuk nilai positif dan negatif.
-
Langkah 3: Hitung Jumlah Nilai
Hitung jumlah nilai dalam kumpulan data. Jumlah nilai adalah banyaknya data dalam kumpulan data tersebut.
-
Langkah 4: Bagi Jumlah dengan Jumlah Nilai
Bagi jumlah dengan jumlah nilai. Hasil pembagian ini adalah mean dari kumpulan data.
Dengan mengikuti langkah-langkah ini, Anda dapat menentukan mean dari setiap kumpulan data. Mean dapat digunakan untuk membandingkan kumpulan data yang berbeda, mengidentifikasi tren, dan membuat prediksi. Memahami cara menentukan mean sangat penting untuk analisis data yang efektif dan pengambilan keputusan yang tepat.
Tips Menentukan Mean
Menentukan mean atau rata-rata sangat penting dalam analisis data. Berikut adalah beberapa tips untuk menentukan mean secara efektif:
Tip 1: Verifikasi Data
Sebelum menentukan mean, pastikan data yang digunakan lengkap, akurat, dan relevan. Data yang tidak lengkap atau tidak akurat dapat menghasilkan mean yang menyesatkan.
Tip 2: Gunakan Rumus yang Tepat
Rumus untuk menentukan mean adalah jumlah semua nilai dibagi dengan jumlah nilai. Pastikan untuk menggunakan rumus ini dengan benar untuk mendapatkan hasil yang akurat.
Tip 3: Pertimbangkan Nilai Ekstrem
Nilai ekstrem dapat memengaruhi mean secara signifikan. Pertimbangkan dampak nilai ekstrem pada mean dan sesuaikan analisis jika diperlukan.
Tip 4: Gunakan Teknologi untuk Menghitung Mean
Perangkat lunak seperti Microsoft Excel atau perangkat statistik khusus dapat digunakan untuk menghitung mean secara otomatis. Ini dapat menghemat waktu dan mengurangi risiko kesalahan.
Tip 5: Interpretasikan Mean dengan Hati-hati
Mean hanyalah salah satu ukuran kecenderungan sentral. Pertimbangkan faktor lain seperti median dan modus saat menafsirkan data.
Dengan mengikuti tips ini, Anda dapat menentukan mean secara akurat dan efektif, memberikan dasar yang kuat untuk analisis data dan pengambilan keputusan.
Kesimpulan Tentang “Cara Menentukan Mean”
Dalam artikel ini, kita telah membahas secara mendalam tentang “cara menentukan mean” dan pentingnya dalam analisis data. Mean, atau rata-rata, adalah ukuran tendensi sentral yang digunakan untuk meringkas kumpulan data dengan nilai tunggal yang mewakili nilai tipikal. Kita telah mempelajari langkah-langkah untuk menentukan mean, tips untuk melakukannya secara efektif, dan hubungannya dengan tren, pengambilan keputusan, dan statistik inferensial.
Memahami cara menentukan mean sangat penting untuk memperoleh wawasan yang berharga dari data. Ini memungkinkan kita untuk membandingkan kumpulan data yang berbeda, mengidentifikasi tren, membuat prediksi, dan membuat keputusan yang tepat berdasarkan bukti. Mean adalah dasar dari banyak teknik statistik, membuka pintu bagi analisis data yang lebih komprehensif dan pengambilan keputusan yang lebih cerdas.
Youtube Video: